/Szkoła średnia/Ciągi

Zadanie nr 6422986

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta prostokątnego o polu 96 tworzą ciąg arytmetyczny. Oblicz:

  • długości boków tego trójkąta,
  • pole koła wpisanego w ten trójkąt.

Rozwiązanie

Oznaczmy szukane boki trójkąta przez 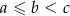a ≤ b < c .

PIC

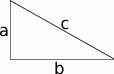
  • Ponieważ boki trójkąta tworzą ciąg arytmetyczny mamy 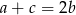a+ c = 2b . Z informacji o polu mamy 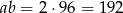ab = 2⋅96 = 192 . Mamy zatem układ równań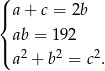
    ( |{ a + c = 2b ab = 192 |( 2 2 2 a + b = c .

    Aby rozwiązać ten układ spróbujmy na początek pozbyć się jednej z niewiadomych (chcemy uprościć sytuację do układu dwóch równań z dwoma niewiadomymi). Najłatwiej pozbyć się c . Podstawiamy za c z pierwszego równania do trzeciego i mamy

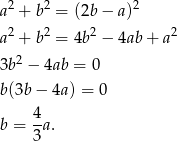
    a 2 + b2 = (2b − a)2 2 2 2 2 a + b = 4b − 4ab+ a 3b 2 − 4ab = 0 b (3b − 4a) = 0 4 b = -a. 3

    Podstawiamy otrzymaną wartość 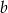b do równania 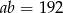ab = 192 i mamy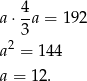

    4 a⋅--a = 192 3 a2 = 144 a = 12.

    Stąd 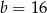b = 16 i c = 20 .  
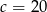    Odpowiedź: 12, 16 i 20

  • Promień okręgu wpisanego w trójkąt możemy wyliczyć ze wzoru na pole 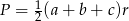1 P = 2(a+ b+ c)r . W naszej sytuacji mamy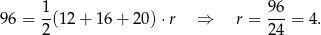
    96 = 1-(12+ 16+ 20) ⋅r ⇒ r = 96-= 4. 2 24

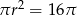    Zatem pole koła wpisanego w trójkąt wynosi πr 2 = 16π .  
    Odpowiedź: 16π

Wersja PDF