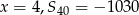/Szkoła średnia/Ciągi

Zadanie nr 6464862

Dodaj do ulubionych
Dodaj do rozwiązanych

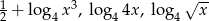Liczby 1 3 √ -- 2 + lo g4x , log44x , log 4 x w podanej kolejności, dla pewnej rzeczywistej wartości x , są trzema kolejnymi początkowymi wyrazami nieskończonego ciągu arytmetycznego. Wyznacz x oraz sumę czterdziestu początkowych wyrazów tego ciągu.

Rozwiązanie

Ze względu na dziedzinę logarytmów musimy mieć oczywiście 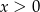x > 0 . W ciągu arytmetycznym 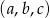(a,b,c) spełniony jest warunek 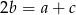2b = a + c , co w naszej sytuacji daje równanie.

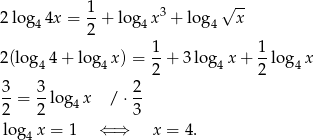
2log 4x = 1-+ lo g x3 + log √x-- 4 2 4 4 1 1 2(lo g44 + log4 x) = --+ 3 log4 x+ --log 4x 2 2 3-= 3log x / ⋅ 2- 2 2 4 3 log4x = 1 ⇐ ⇒ x = 4.

Zatem początkowe wyrazu danego ciągu to

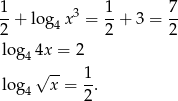
1- 3 1- 7- 2 + log4 x = 2 + 3 = 2 log 4x = 2 4 √ -- 1- log4 x = 2 .

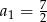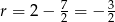Mamy więc do czynienia z ciągiem, w którym a1 = 72 i r = 2 − 72 = − 32 . Zatem

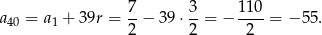
7- 3- 1-10 a40 = a1 + 39r = 2 − 39⋅ 2 = − 2 = − 55.

Stąd

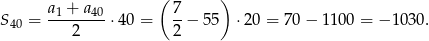
( ) S40 = a1-+-a40 ⋅40 = 7-− 55 ⋅20 = 7 0− 1100 = − 103 0. 2 2

 
Odpowiedź: x = 4,S40 = − 1030

Wersja PDF