/Szkoła średnia/Ciągi

Zadanie nr 6537763

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj, czy ciąg 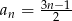3n−1- an = 2 jest arytmetyczny.

Rozwiązanie

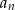Aby sprawdzić czy ciąg jest arytmetyczny musimy sprawdzić, czy różnica jego dwóch kolejnych wyrazów jest stała, tzn. nie zależy od n . Inny, prostszy sposób, to skorzystać z faktu, że jeżeli an jest ciągiem arytmetycznym to 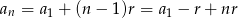an = a + (n − 1)r = a − r+ nr 1 1 . Zatem jeżeli wzór definiujący ciąg nie jest postaci 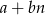a + bn , to ciąg nie jest arytmetyczny.

Z metody ze wzorem widać, że ciąg jest arytmetyczny, ale dla pewności policzmy

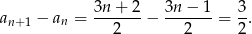
an+1 − an = 3n+--2-− 3n-−--1 = 3-. 2 2 2

Różnica ta nie zależy od n , zatem ciąg jest arytmetyczny.  
Odpowiedź: Tak, jest to ciąg arytmetyczny.

Wersja PDF