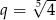/Szkoła średnia/Ciągi

Zadanie nr 6582828

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz iloraz niezerowego ciągu geometrycznego, w którym suma 10 początkowych wyrazów jest 5 razy większa od sumy pierwszych 5 wyrazów.

Rozwiązanie

Sposób I

Jeżeli oznaczymy kolejne wyrazy szukanego ciągu przez 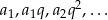2 a1,a1q,a2q ,... , to mamy

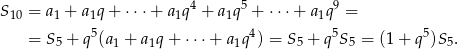
4 5 9 S10 = a1 + a1q+ ⋅⋅⋅+ a1q + a 1q + ⋅⋅ ⋅+ a1q = = S + q5(a + a q + ⋅⋅⋅+ a q4) = S + q5S = (1 + q5)S . 5 1 1 1 5 5 5

Z drugiej strony wiemy, że 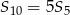S 10 = 5S5 , zatem

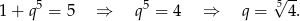
√ -- 1 + q5 = 5 ⇒ q5 = 4 ⇒ q = 5 4.

Sposób II

Tym razem skorzystamy ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego.

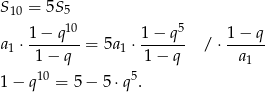
S = 5S 10 5 1−--q10 1-−-q5- 1−--q- a1 ⋅ 1− q = 5a1 ⋅ 1− q /⋅ a 1 1− q10 = 5− 5⋅ q5.

Zanim przejdziemy dalej, zauważmy, że cały powyższy rachunek ma sens o ile 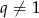q ⁄= 1 . Jednak jest jasne, że ten przypadek nie może zachodzić (bo ciąg jest niezerowy). Podstawiamy teraz 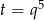5 t = q i mamy równanie

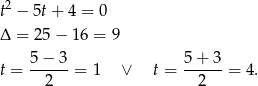
t2 − 5t+ 4 = 0 Δ = 25 − 16 = 9 5 − 3 5 + 3 t = ------= 1 ∨ t = ------= 4. 2 2

Zatem

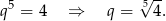
-- q5 = 4 ⇒ q = 5√ 4.

Sposób III

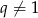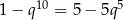Tak jak w poprzednim sposobie zauważamy, że q ⁄= 1 i1 − q10 = 5 − 5q 5 . Mamy zatem

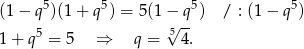
5 5 5 5 (1 − q )(1 + q ) = 5(1 −√ q-) / : (1− q ) 1 + q5 = 5 ⇒ q = 5 4.

 
Odpowiedź: √5 -- q = 4

Wersja PDF