Zadanie nr 6596024
Wykaż, że jeżeli 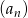 jest ciągiem geometrycznym, to ciąg
jest ciągiem geometrycznym, to ciąg 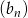 o wyrazie ogólnym określonym wzorem
o wyrazie ogólnym określonym wzorem 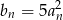 też jest ciągiem geometrycznym.
też jest ciągiem geometrycznym.
Rozwiązanie
Jeżeli ciąg 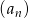 jest ciągiem zerowym to taki sam jest ciąg
jest ciągiem zerowym to taki sam jest ciąg 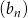 , więc możemy założyć, że mamy do czynienia z ciągami bez zer.
, więc możemy założyć, że mamy do czynienia z ciągami bez zer.
Oznaczmy iloraz ciągu 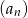 przez
przez 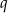 . Obliczmy iloraz kolejnych wyrazów ciągu
. Obliczmy iloraz kolejnych wyrazów ciągu 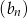 (musimy sprawdzić, że jest on stały).
(musimy sprawdzić, że jest on stały).
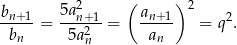
Iloraz ten jest stały (nie zależy od  ), co dowodzi, że ciąg
), co dowodzi, że ciąg 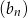 jest geometryczny.
jest geometryczny.

