/Szkoła średnia/Ciągi

Zadanie nr 6626194

Dodaj do ulubionych
Dodaj do rozwiązanych

W dziewięciowyrazowym ciągu arytmetycznym, o pierwszym wyrazie równym 4, wyraz pierwszy, trzeci i siódmy tworzą ciąg geometryczny. Oblicz sumę wyrazów tego ciągu arytmetycznego

Rozwiązanie

Jeżeli oznaczymy przez

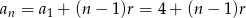
an = a 1 + (n − 1 )r = 4+ (n− 1)r

podany ciąg arytmetyczny to wiemy, że

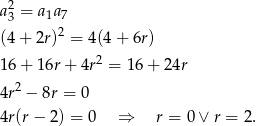
2 a 3 = a1a7 (4 + 2r)2 = 4(4+ 6r) 1 6+ 16r+ 4r2 = 16 + 24r 2 4r − 8r = 0 4r (r− 2) = 0 ⇒ r = 0 ∨ r = 2.

Jeżeli 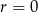r = 0 to ciąg jest stały i suma jego wyrazów wynosi 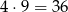4⋅9 = 36 . Jeżeli natomiast 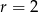r = 2 , to ze wzoru na sumę ciągu arytmetycznego mamy

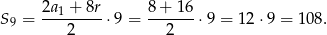
2a 1 + 8r 8+ 16 S9 = ---------⋅9 = -------⋅9 = 12 ⋅9 = 10 8. 2 2

 
Odpowiedź: 36 lub 108

Wersja PDF