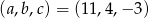Zadanie nr 6661171
Liczby 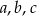 są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby
są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby 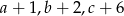 – trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby
– trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby 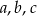 wiedząc, że ich suma jest równa 12.
wiedząc, że ich suma jest równa 12.
Rozwiązanie
Wiemy, że 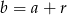 i
i 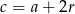 dla pewnej liczby
dla pewnej liczby  . Ponadto
. Ponadto
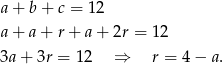
Zatem 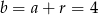 i
i 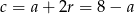 .
.
Pozostało wykorzystać informację o ciągu geometrycznym.
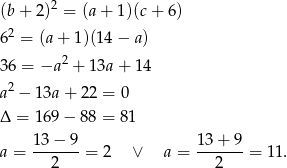
Daje to nam 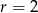 lub
lub 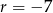 odpowiednio oraz
odpowiednio oraz
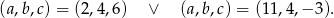
Odpowiedź: 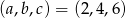 lub
lub