Zadanie nr 6683339
Dany jest ciąg 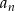 o wyrazie ogólnym
o wyrazie ogólnym 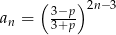 .
.
- Udowodnij, że ciąg
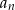 jest ciągiem geometrycznym.
jest ciągiem geometrycznym. - Wyznacz te wartości parametru
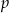 , dla których istnieje suma wszystkich wyrazów ciągu
, dla których istnieje suma wszystkich wyrazów ciągu 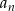 . Oblicz tę sumę.
. Oblicz tę sumę. - Wyznacz te wartości parametru
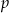 , dla których ciąg
, dla których ciąg 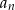 jest malejący.
jest malejący.
Rozwiązanie
Zauważmy, że
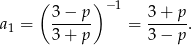
Zatem 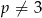 .
.
- Musimy sprawdzić, że iloraz dwóch sąsiednich wyrazów jest stały (nie zależy od
 ).
). 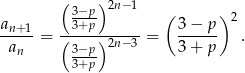
- Z poprzedniego podpunktu wiemy, że
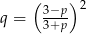 . Musimy sprawdzić, kiedy
. Musimy sprawdzić, kiedy 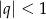 .
. 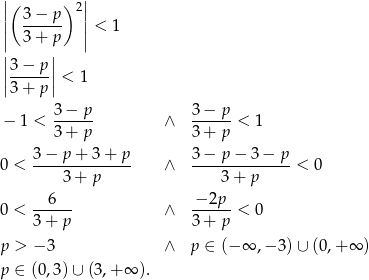
Suma wynosi
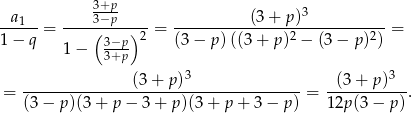
Odpowiedź: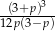
- Sprawdżmy kiedy
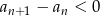 .
. 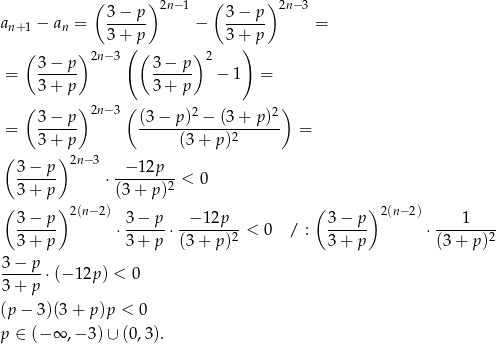
Odpowiedź: