/Szkoła średnia/Ciągi

Zadanie nr 7028666

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma szóstego i szesnastego wyrazu ciągu arytmetycznego 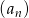(an) jest równa 5, a iloczyn wyrazu ósmego i dwunastego równy jest 3. Wyznacz wzór na wyraz ogólny ciągu (an) .

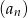Rozwiązanie

Korzystając ze wzoru na wyraz ogólny ciągu arytmetycznego 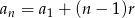an = a1 + (n − 1)r mamy równania

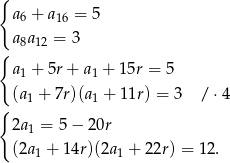
{ a6 + a16 = 5 a a = 3 { 8 12 a1 + 5r+ a1 + 15r = 5 (a1 + 7r)(a1 + 11r) = 3 /⋅ 4 { 2a1 = 5 − 20r (2a1 + 14r)(2a1 + 22r) = 12.

Podstawiamy teraz do drugiego równania wartość 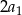2a 1 z pierwszego równania

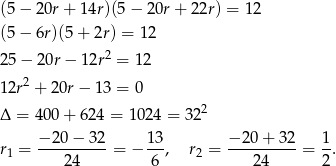
(5 − 20r + 14r)(5 − 20r + 22r) = 1 2 (5 − 6r)(5 + 2r) = 12 25 − 20r − 12r2 = 1 2 12r2 + 20r − 13 = 0 2 Δ = 400 + 624 = 1024 = 32 −-20-−-32- 13- −-20-+-32- 1- r1 = 24 = − 6 , r2 = 24 = 2.

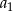Skoro mamy r , to mamy też a1 , bo jak wyliczyliśmy wyżej

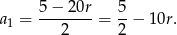
5-−-20r- 5- a1 = 2 = 2 − 10r .

To pozwala nam wyliczyć 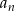an :

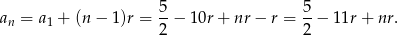
5 5 an = a1 + (n − 1)r = 2 − 10r+ nr− r = 2-− 11r + nr .

Na koniec podstawiamy dwie znalezione wartości r .

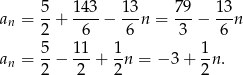
5- 14-3 13- 79- 13- an = 2 + 6 − 6 n = 3 − 6 n 5 11 1 1 an = --− ---+ -n = − 3+ -n . 2 2 2 2

 
Odpowiedź: 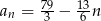79 13 an = 3 − 6 n lub 1 an = − 3+ 2n

Wersja PDF