Zadanie nr 7069524
Wykaż, że dla dowolnego ciągu arytmetycznego zachodzi równość 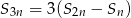 , gdzie
, gdzie 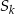 oznacza sumę
oznacza sumę 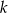 początkowych wyrazów ciągu.
początkowych wyrazów ciągu.
Rozwiązanie
Korzystamy ze wzoru 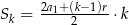 . Liczymy prawą stronę
. Liczymy prawą stronę
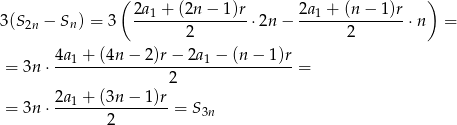
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnego ciągu arytmetycznego zachodzi równość 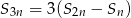 , gdzie
, gdzie 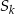 oznacza sumę
oznacza sumę 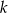 początkowych wyrazów ciągu.
początkowych wyrazów ciągu.
Korzystamy ze wzoru 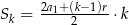 . Liczymy prawą stronę
. Liczymy prawą stronę