Zadanie nr 7073513
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny, w którym środkowy wyraz jest równy 8. Wyznacz długości boków trójkąta, oblicz jego pole oraz promień okręgu opisanego na tym trójkącie.
Rozwiązanie
Skoro długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego, możemy je oznaczyć przez 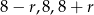 .
.
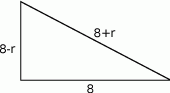
Różnicę  wyliczymy zapisując twierdzenie Pitagorasa
wyliczymy zapisując twierdzenie Pitagorasa
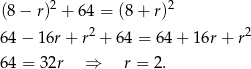
Zatem mamy do czynienia z trójkątem o bokach 6,8,10 i jego pole jest równe
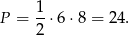
Promień okręgu opisanego na trójkącie prostokątnym to dokładnie połowa długości przeciwprostokątnej, czyli
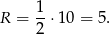
Odpowiedź: Boki: 6,8,10, pole: 24, promień: 5.

