Zadanie nr 7172985
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 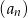 wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
- Oblicz pierwszy wyraz i iloraz ciągu geometrycznego
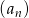 .
. - Sprawdź czy istnieje takie
 , dla którego
, dla którego ![2√2[(1+ √2)2−3] an = 5(√3+-1)(√-3−-1)](https://img.zadania.info/zad/7172985/HzadT3x.gif) .
. - Jakie dwie liczby
 i
i 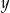 należy wstawić między pierwszy i trzeci wyraz ciągu
należy wstawić między pierwszy i trzeci wyraz ciągu 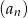 , aby ciąg
, aby ciąg 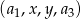 był ciągiem arytmetycznym?
był ciągiem arytmetycznym?
Rozwiązanie
- Ze wzorów na sumę początkowych oraz wszystkich wyrazów ciągu geometrycznego otrzymujemy układ równań.
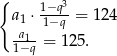
Podstawiając za
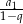 w pierwszym równaniu otrzymujemy
w pierwszym równaniu otrzymujemy 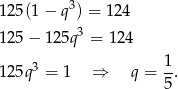
Zatem
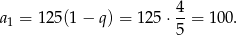
Odpowiedź: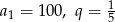
- Przekształćmy najpierw podane wyrażenie (korzystając ze wzorów skróconego mnożenia).
![√ --[ √ -- ] √ -[ √ -- ] 2 2 (1+ 2)2 − 3 2 2 1+ 2 2+ 2− 3 ---√--------√-------- = ------------------------= -8- = 4-. 5( 3 + 1)( 3 − 1) 5(3 − 1) 1 0 5](https://img.zadania.info/zad/7172985/HzadR5x.gif)
Musimy więc rozwiązać równanie
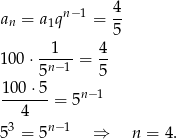
Odpowiedź: Istnieje,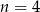
- Pytanie brzmi dla jakich
 i
i 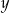 ciąg
ciąg 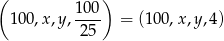
jest arytmetyczny. Tak będzie, gdy
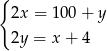
(wyrazy
 i
i 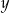 muszą być średnimi arytmetycznymi sąsiednich wyrazów). Dodajemy do pierwszego równania dwa razy drugie (żeby skrócić
muszą być średnimi arytmetycznymi sąsiednich wyrazów). Dodajemy do pierwszego równania dwa razy drugie (żeby skrócić  ) i mamy
) i mamy 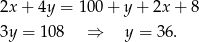
Zatem
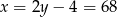 .
.
Odpowiedź: