/Szkoła średnia/Ciągi

Zadanie nr 7229030

Dodaj do ulubionych
Dodaj do rozwiązanych

Czwarty wyraz ciągu arytmetycznego jest równy 8. Suma pięciu pierwszych wyrazów tego ciągu jest równa 15. Oblicz siódmy wyraz tego ciągu.

Rozwiązanie

Zapisujemy podane informacje w postaci układu równań

{ 8 = a 4 = a1 + 3r 15 = a1 + a 2 + a3 + a4 + a5 = a1 + (a1 + r)+ (a1 + 2r )+ a4 + (a4 + r).

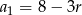Zatem a1 = 8 − 3r i drugie równanie przybiera postać

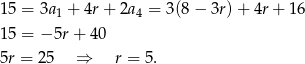
15 = 3a1 + 4r+ 2a 4 = 3(8− 3r)+ 4r+ 16 15 = −5r + 40 5r = 25 ⇒ r = 5.

Zatem

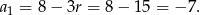
a1 = 8 − 3r = 8− 15 = − 7.

Teraz już łatwo obliczyć siódmy wyraz ciągu

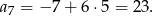
a 7 = − 7+ 6⋅5 = 23.

 
Odpowiedź: 23

Wersja PDF