/Szkoła średnia/Ciągi

Zadanie nr 7301954

Dodaj do ulubionych
Dodaj do rozwiązanych

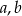Długość krawędzi bocznej c prostopadłościennego pudełka o podstawie prostokąta tworzy wraz z długościami krawędzi podstawy a,b (w kolejności 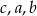c,a,b ) ciąg artymetyczny o różnicy -2.

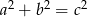  • Oblicz długości krawędzi pudełka, jeśli a2 + b 2 = c2 .
  • Wyznacz miarę kąta nachylenia przekątnej pudełka do płaszczyzny podstawy.

Rozwiązanie

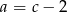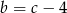  • Z podanych informacji wiemy, że a = c− 2 i b = c− 4 . Dodatkowo wiemy, że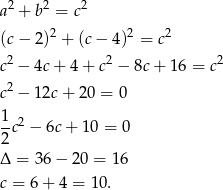
    a2 + b2 = c2 2 2 2 (c − 2) + (c− 4) = c 2 2 2 c − 4c + 4+ c − 8c+ 1 6 = c c2 − 12c + 20 = 0 1-c2 − 6c+ 1 0 = 0 2 Δ = 36 − 20 = 16 c = 6 + 4 = 10.

    Zatem 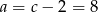a = c− 2 = 8 i b = c − 4 = 6 .  
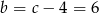    Odpowiedź: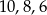 10,8,6

  • Robimy rysunek.
    PIC

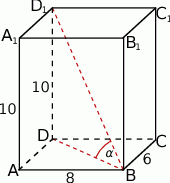
    Obliczamy na początek długość przekątnej podstawy.

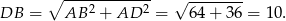
    ∘ ---2-------2 √ -------- DB = AB + AD = 64 + 36 = 10 .

    Zatem trójkąt 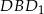DBD 1 jest prostokątny i równoramienny, więc szukany kąt jest równy 45∘ .  
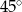    Odpowiedź: ∘ 45

Wersja PDF