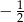Zadanie nr 7323377
Miary pięciu kątów tworzą ciąg arytmetyczny. Drugim wyrazem tego ciągu jest 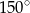 , a czwartym
, a czwartym 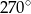 . Oblicz sumę sinusów tych pięciu kątów.
. Oblicz sumę sinusów tych pięciu kątów.
Rozwiązanie
Ze wzoru na  -ty wyraz ciągu arytmetycznego mamy
-ty wyraz ciągu arytmetycznego mamy
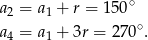
Odejmując od drugiej równości pierwszą (żeby skrócić 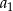 ) mamy
) mamy
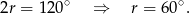
Zatem 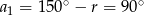 i ciąg, o którym mowa to
i ciąg, o którym mowa to
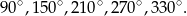
Pozostało obliczyć sumę sinusów
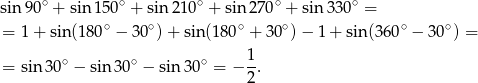
Odpowiedź: