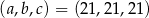/Szkoła średnia/Ciągi

Zadanie nr 7337200

Dodaj do ulubionych
Dodaj do rozwiązanych

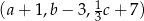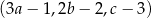Ciąg (a,b,c) jest geometryczny, a ciągi 1 (a + 1,b − 3,3c + 7) i (3a − 1,2b − 2 ,c− 3) są arytmetyczne. Oblicz a,b,c .

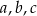Rozwiązanie

W ciągu geometrycznym kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich, a w ciągu arytmetycznym wyraz środkowy jest średnią arytmetyczną wyrazów sąsiednich. Mamy więc układ równań

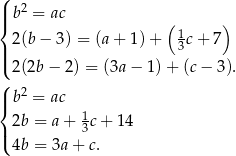
( || b 2 = ac { (1 ) | 2 (b− 3) = (a+ 1)+ 3c + 7 |( 2 (2b− 2) = (3a − 1) + (c− 3). ( |{ b 2 = ac 1 | 2b = a+ 3c + 14 ( 4b = 3a + c.

Podstawiamy 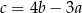c = 4b − 3a z trzeciego równania do dwóch pierwszych.

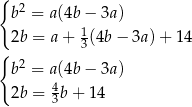
{ b2 = a(4b− 3a) 1 2b = a+ 3(4b − 3a) + 14 { 2 b = a(4b− 3a) 2b = 43b + 14

Z drugiego równania mamy

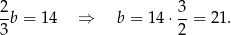
2- 3- 3b = 14 ⇒ b = 14⋅ 2 = 21.

Podstawiamy teraz tę wartość do pierwszego równania.

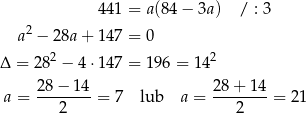
44 1 = a(84 − 3a) / : 3 a2 − 28a + 14 7 = 0 2 2 Δ = 28 − 4⋅14 7 = 196 = 14 28 − 14 28 + 14 a = --------= 7 lub a = --------= 21 2 2

W pierwszym przypadku mamy

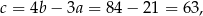
c = 4b − 3a = 84− 21 = 63,

a w drugim

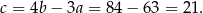
c = 4b − 3a = 84− 63 = 21.

 
Odpowiedź: 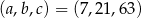(a,b,c) = (7 ,21,63) lub (a,b,c) = (2 1,21,21)

Wersja PDF