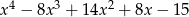Zadanie nr 7355736

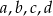Pierwiastkami wielomianu czwartego stopnia W (x ) są liczby a ,b,c,d , które w podanej kolejności tworzą ciąg arytmetyczny o różnicy 2. Suma pierwiastków równa jest 8.

Oblicz pierwiastk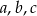i i .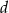
Wiedząc że 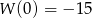, przedstaw wielomian w postaci .

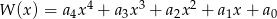Rozwiązanie

Wiemy, że
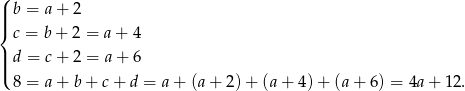
$( || b = a+ 2 |{ c = b+ 2 = a + 4 ||| d = c+ 2 = a + 6 ( 8 = a+ b+ c+ d = a+ (a+ 2)+ (a+ 4 )+ (a + 6) = 4a+ 12.$

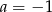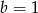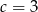Zatem , , i .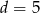
Odpowiedź: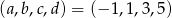
Z poprzedniego podpunktu wiemy, że
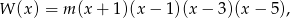
$W (x) = m (x + 1)(x − 1 )(x− 3)(x− 5),$

dla pewnej stałej 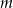. Wartość 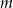możemy wyznaczyć z podanego warunku .

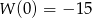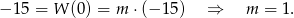
$− 15 = W (0) = m ⋅(− 15) ⇒ m = 1.$

Pozostało wymnożyć nawiasy z prawej strony równości

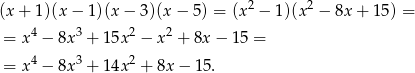
$2 2 (x + 1)(x − 1)(x − 3 )(x− 5) = (x − 1)(x − 8x + 15 ) = = x 4 − 8x 3 + 1 5x2 − x2 + 8x − 15 = 4 3 2 = x − 8x + 1 4x + 8x − 15.$

Odpowiedź: