/Szkoła średnia/Ciągi

Zadanie nr 7512764

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest nieskończony ciąg sześcianów 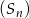(Sn ) określony dla 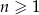n ≥ 1 . Krawędź pierwszego z nich jest równa 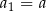a1 = a . Krawędź drugiego z tych sześcianów ma długość 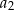a2 równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź 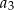a 3 o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg (Sn ) .

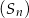Rozwiązanie

Naszkicujmy sześcian.

PIC

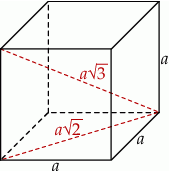
Pole powierzchni pierwszego sześcianu jest równe 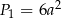P 1 = 6a2 .

Drugi sześcian w opisanym ciągu ma krawędź długości

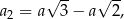
√ -- √ -- a2 = a 3− a 2,

więc jego pole powierzchni jest równe

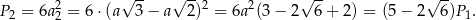
√ -- √ -- √ -- √ -- P2 = 6a22 = 6 ⋅(a 3− a 2)2 = 6a2(3 − 2 6 + 2 ) = (5− 2 6)P1.

Analogicznie, pole trzeciego sześcianu będzie równe

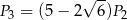
√ -- P3 = (5 − 2 6)P2

i tak dalej. Pola powierzchni tworzą więc ciąg geometryczny o pierwszym wyrazie 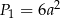P1 = 6a 2 i ilorazie 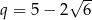√ -- q = 5− 2 6 . Suma wszystkich wyrazów tego ciągu jest równa

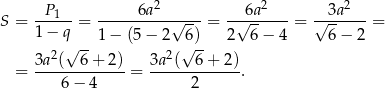
P1 6a 2 6a2 3a2 S = ------= ----------√----= -√-------= √-------= 1 − q√ -- 1− (5− 2 √6)- 2 6− 4 6− 2 3a2( 6 + 2) 3a2( 6 + 2) = -------------= -------------. 6− 4 2

 
Odpowiedź: 3 2√ -- 2a ( 6+ 2 )

Wersja PDF