/Szkoła średnia/Ciągi

Zadanie nr 7658585

Dodaj do ulubionych
Dodaj do rozwiązanych

W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 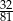3281- . Jaka jest suma wyrazów tego ciągu?

Rozwiązanie

Jeżeli oznaczymy dany ciąg przez 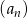(an) , to mamy 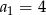a1 = 4 i

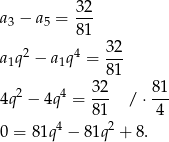
32 a3 − a5 = --- 81 a q 2 − a q4 = 32- 1 1 81 2 4 32 81 4q − 4q = 81- / ⋅-4- 4 2 0 = 81q − 81q + 8.

Otrzymane równanie jest dwukwadratowe, więc podstawmy 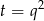t = q2 .

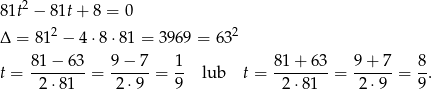
2 8 1t − 81t + 8 = 0 Δ = 812 − 4 ⋅8 ⋅81 = 396 9 = 632 t = 81−--63-= 9−--7-= 1- lub t = 81-+-63-= 9+--7-= 8. 2⋅ 81 2 ⋅9 9 2 ⋅81 2 ⋅9 9

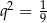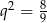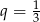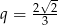Mamy stąd q2 = 1 9 lub q2 = 8 9 . Ponieważ ciąg ma mieć wyrazy dodatnie, mamy q = 13 lub √- q = 232- . Suma szeregu 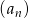(an ) jest więc równa

S = --a1--= --4---= 4-= 6. 1 − q 1 − 13 23

lub

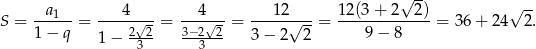
√ -- √ -- S = --a1--= ---4-√--= --4√-- = ---12√---= 12(3+--2--2)-= 3 6+ 24 2. 1 − q 1− 2-2- 3−-2-2 3− 2 2 9 − 8 3 3

 
Odpowiedź: 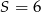S = 6 lub √ -- S = 36 + 24 2

Wersja PDF