/Szkoła średnia/Ciągi

Zadanie nr 7762227

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnić, że w dowolnym trójkącie prostokątnym, w którym długości boków tworzą ciąg arytmetyczny, promień okręgu wpisanego w ten trójkąt jest równy różnicy ciągu długości jego boków.

Rozwiązanie

Oznaczmy boki trójkąta przez 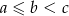a ≤ b < c . Mamy zatem 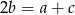2b = a+ c . Promień okręgu wpisanego w trójkąt możemy obliczyć ze wzoru na pole

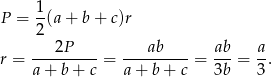
P = 1-(a+ b+ c)r 2 2P ab ab a r = ---------= --------- = ---= -. a+ b+ c a + b + c 3b 3

Pozostało uzasadnić, że 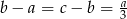b − a = c− b = a 3 . Na mocy twierdzenia Pitagorasa mamy

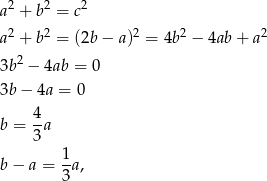
2 2 2 a + b = c a2 + b2 = (2b− a)2 = 4b2 − 4ab + a2 2 3b − 4ab = 0 3b− 4a = 0 b = 4-a 3 1- b− a = 3a ,

co kończy dowód.

Wersja PDF