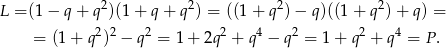/Szkoła średnia/Ciągi

Zadanie nr 7784893

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że jeżeli liczby 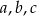a,b,c są kolejnymi wyrazami ciągu geometrycznego, to

(a − b + c)(a + b + c) = a2 + b2 + c2.

Rozwiązanie

Sposób I

Przekształcamy lewą stronę równości, którą mamy udowodnić (korzystamy ze wzoru na różnicę kwadratów).

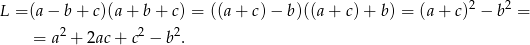
2 2 L = (a− b+ c)(a + b + c) = ((a + c) − b)((a + c)+ b) = (a + c) − b = = a2 + 2ac+ c2 − b 2.

Wiemy ponadto, liczby 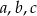a,b,c są kolejnymi wyrazami ciągu geometrycznego, więc 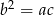b2 = ac . Mamy zatem

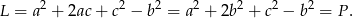
L = a2 + 2ac + c2 − b2 = a2 + 2b2 + c2 − b2 = P .

Sposób II

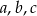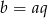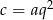Skoro liczby a,b,c są kolejnymi wyrazami ciągu geometrycznego, to b = aq i c = aq 2 dla pewnego 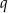q . Równość, którą mamy udowodnić przyjmuje więc postać.

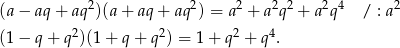
2 2 2 2 2 2 4 2 (a− aq + aq )(a+ aq + aq ) = a + a q + a q / : a (1− q + q2)(1 + q + q2) = 1 + q 2 + q4.

Aby udowodnić tę równość przekształcamy lewą stronę (korzystamy ze wzoru na różnicę kwadratów).

L = (1 − q + q2)(1 + q + q2) = ((1 + q2) − q)((1 + q2) + q) = = (1+ q 2)2 − q2 = 1 + 2q 2 + q 4 − q2 = 1+ q 2 + q4 = P.
Wersja PDF