/Szkoła średnia/Ciągi

Zadanie nr 7850322

Dodaj do ulubionych
Dodaj do rozwiązanych

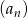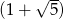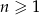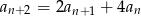Iloraz ciągu geometrycznego (an) jest równy √ -- (1 + 5) . Uzasadnij, że dla każdej liczby naturalnej n ≥ 1 prawdziwy jest wzór an+ 2 = 2an+1 + 4an .

Rozwiązanie

Korzystamy ze wzoru 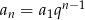n−1 an = a 1q na n –ty wyraz ciągu geometrycznego.

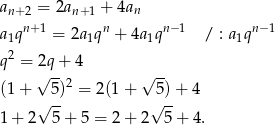
a = 2a + 4a n+ 2 n+1 n a1qn+ 1 = 2a1qn + 4a1qn− 1 / : a1qn− 1 2 q = 2q-+ 4 -- (1 + √ 5)2 = 2(1 + √ 5 )+ 4 √ -- √ -- 1 + 2 5 + 5 = 2 + 2 5+ 4.

Otrzymana równość jest oczywiście prawdziwa, więc wyjściowa równość też musi być spełniona.

Wersja PDF