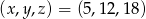/Szkoła średnia/Ciągi

Zadanie nr 7908396

Dodaj do ulubionych
Dodaj do rozwiązanych

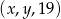Ciąg (x ,y,19) jest arytmetyczny, a ciąg 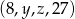(8,y,z,27) jest geometryczny. Oblicz 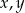x ,y oraz z .

Rozwiązanie

Jeżeli 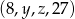(8,y ,z,27) jest ciągiem geometrycznym o ilorazie 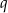q to

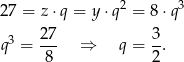
2 3 27 = z⋅q = y⋅ q = 8⋅ q 3 27- 3- q = 8 ⇒ q = 2.

Stąd

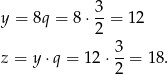
y = 8q = 8 ⋅ 3-= 12 2 3 z = y⋅ q = 12 ⋅2-= 18.

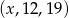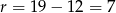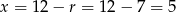Wiemy zatem, że ciąg (x ,12,19) jest arytmetyczny. Jego różnica jest równa r = 1 9− 1 2 = 7 . Stąd x = 12 − r = 12 − 7 = 5 .  
Odpowiedź: (x ,y ,z) = (5,12,18)

Wersja PDF