Zadanie nr 7934653

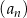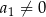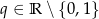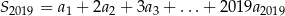Ciąg (an ) jest geometryczny o wyrazie pierwszym równym a1 ⁄= 0 i ilorazie q ∈ R ∖{ 0,1} , Oblicz sumę S 2019 = a 1 + 2a 2 + 3a 3 + ...+ 2019a2019 .

Rozwiązanie

Musimy obliczyć sumę

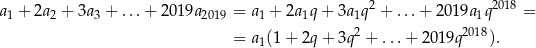
2 2018 a1 + 2a2 + 3a3 + ...+ 20 19a2019 = a1 + 2a1q+ 3a1q + ...+ 201 9a1q = = a1(1+ 2q+ 3q2 + ...+ 201 9q2018).

Sposób I

Korzystamy ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego.

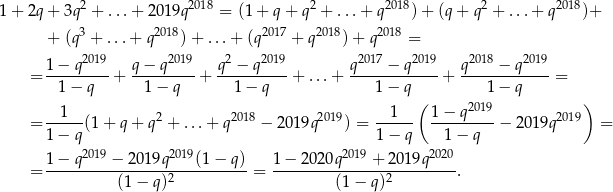
1+ 2q+ 3q2 + ...+ 20 19q2018 = (1+ q+ q 2 + ...+ q2018) + (q + q2 + ...+ q 2018)+ + (q3 + ...+ q2018)+ ...+ (q2017 + q 2018)+ q2018 = 2019 2019 2 2019 2017 2019 2018 2019 = 1-−-q---- + q-−-q----+ q-−--q----+ ... + q----−--q----+ q-----−-q----= 1 − q 1− q 1 − q 1− q 1 − q 1 1 ( 1 − q2019 ) = ------(1+ q + q2 + ...+ q2018 − 201 9q2019) = ------ --------- − 2019q 2019 = 1 − q 1− q 1 − q 1 − q2019 − 2019q2019(1− q) 1 − 2 020q2019 + 2 019q2020 = -----------------2---------- = ----------------2---------. (1 − q) (1 − q)

Interesująca nas suma jest więc równa

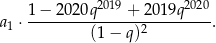
1 − 2020q 2019 + 2019q 2020 a1 ⋅-------------------------. (1− q )2

Sposób II

Rozważmy funkcję

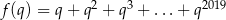
2 3 2019 f (q) = q+ q + q + ...+ q

określoną dla 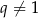q ⁄= 1 . Obliczymy pochodną tej funkcji na dwa sposoby. Z jednej strony

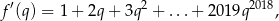
f′(q) = 1 + 2q + 3q2 + ...+ 2 019q2018,

a z drugiej

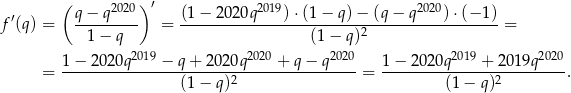
( ) ′ q − q2020 ′ (1− 2 020q2019)⋅(1 − q) − (q − q2020)⋅(− 1) f (q) = --1−--q-- = -----------------(1-−-q)2-------------------= 1-−-202-0q2019-−-q-+-202-0q2020-+-q-−-q2020 1-−-20-20q2019-+-20-19q2020- = (1 − q)2 = (1− q)2 .

Udowodniliśmy więc, że

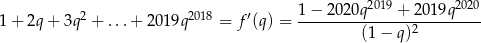
2 2018 ′ 1−--2020q-2019 +-2019q-2020- 1+ 2q+ 3q + ...+ 201 9q = f (q ) = (1 − q )2

i interesująca nas suma jest równa

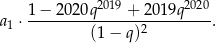
2019 2020 a1 ⋅ 1-−-2020q----+-2019q----. (1− q )2

Odpowiedź: a1 ⋅ 1−2020q2019+-2019q2020 (1−q)2