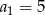/Szkoła średnia/Ciągi

Zadanie nr 7995704

Dodaj do ulubionych
Dodaj do rozwiązanych

Iloraz ciągu geometrycznego 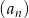(an) , gdzie 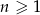n ≥ 1 jest równy 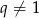q ⁄= 1 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek 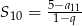S10 = 5−1a−q11 . Oblicz pierwszy wyraz tego ciągu.

Rozwiązanie

Korzystamy ze wzoru

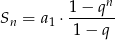
1− qn Sn = a1 ⋅------- 1 − q

na sumę n początkowych wyrazów ciągu geometrycznego. Mamy zatem

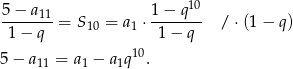
10 5-−-a11 1−--q-- 1 − q = S 10 = a1 ⋅ 1 − q / ⋅(1 − q) 10 5− a11 = a1 − a1q .

Ponieważ 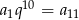a1q 10 = a11 , otrzymujemy stąd a1 = 5 .  
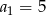Odpowiedź: a1 = 5

Wersja PDF