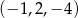Zadanie nr 8105181
Trzy liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 9, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Rozwiązanie
Dane liczby możemy zapisać w postaci: 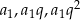 . Jest jednak mały kłopot, bo nie wiemy, która z tych liczb jest najmniejsza. Na szczęście wiemy, że
. Jest jednak mały kłopot, bo nie wiemy, która z tych liczb jest najmniejsza. Na szczęście wiemy, że 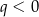 , więc są dwie możliwości: jeżeli
, więc są dwie możliwości: jeżeli 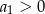 , to najmniejsza jest druga liczba, a jeżeli
, to najmniejsza jest druga liczba, a jeżeli 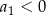 , to najmniejsza jest trzecia liczba (bo
, to najmniejsza jest trzecia liczba (bo 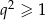 ).
).
Zajmijmy się najpierw przypadkiem, gdy 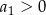 . Wtedy wiemy, że ciąg
. Wtedy wiemy, że ciąg 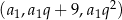 jest arytmetyczny, czyli
jest arytmetyczny, czyli
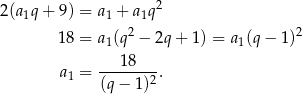
Z założenia 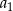 i
i 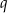 są liczbami całkowitymi, więc
są liczbami całkowitymi, więc 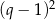 jest kwadratem liczby całkowitej dzielącym 18. Zatem
jest kwadratem liczby całkowitej dzielącym 18. Zatem 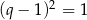 lub
lub 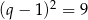 , czyli
, czyli
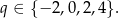
Interesują nas jednak tylko ujemne wartości 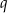 , więc
, więc 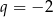 ,
, 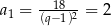 i szukane liczby to
i szukane liczby to
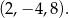
Zajmijmy się teraz drugim przypadkiem, gdy 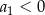 . Wtedy arytmetyczny jest ciąg
. Wtedy arytmetyczny jest ciąg 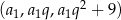 , więc
, więc
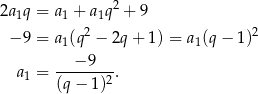
Tak jak poprzednio wnioskujemy stąd, że 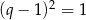 lub
lub 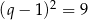 , czyli
, czyli
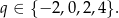
Tak jak poprzednio mamy stąd 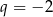 i
i 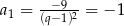 . Otrzymujemy więc w tym przypadku ciąg
. Otrzymujemy więc w tym przypadku ciąg
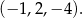
Odpowiedź: 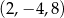 lub
lub