/Szkoła średnia/Ciągi

Zadanie nr 8108128

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 21, a cosinus największego kąta jest równy 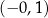(− 0,1) . Oblicz długości boków tego trójkąta.

Rozwiązanie

Zacznijmy od szkicowego rysunku i oznaczmy boki trójkąta przez 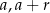a,a+ r i a + 2r .

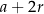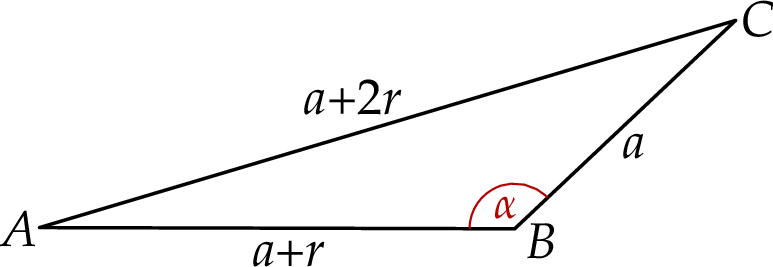
ZINFO-FIGURE

Ponieważ w trójkącie naprzeciw większego kąta leży większy bok, kąt o cosinusie 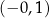(− 0,1) leży naprzeciw boku długości 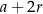a+ 2r . Z podanego obwodu mamy

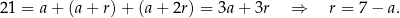
2 1 = a+ (a+ r)+ (a + 2r) = 3a+ 3r ⇒ r = 7 − a.

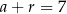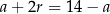Zatem boki trójkąta mają długości a , a + r = 7 i a + 2r = 14− a . Napiszmy teraz twierdzenie cosinusów.

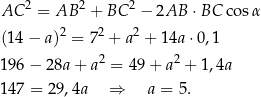
AC 2 = AB 2 + BC 2 − 2AB ⋅ BC cos α 2 2 2 (14 − a) = 7 + a + 14a ⋅0,1 196 − 28a + a 2 = 49+ a2 + 1,4a 147 = 29,4a ⇒ a = 5.

 
Odpowiedź: 5, 7, 9

Wersja PDF