/Szkoła średnia/Ciągi

Zadanie nr 8124430

Dodaj do ulubionych
Dodaj do rozwiązanych

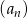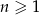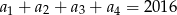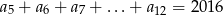Dany jest ciąg arytmetyczny (an ) określony dla każdej liczby naturalnej n ≥ 1 , w którym a1 + a2 + a 3 + a4 = 2 016 oraz a5 + a6 + a7 + ...+ a12 = 2016 . Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu (an) .

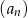Rozwiązanie

Korzystamy ze wzoru

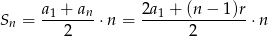
a + a 2a + (n − 1)r Sn = -1----n-⋅n = --1------------⋅n 2 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

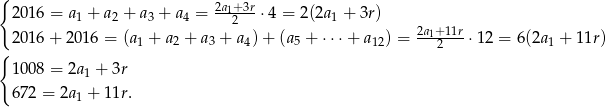
{ 2a1+ 3r 201 6 = a1 + a2 + a3 + a 4 =--2---⋅4 = 2 (2a1 + 3r) 201 6+ 2 016 = (a1 + a2 + a3 + a4)+ (a5 + ⋅ ⋅⋅+ a12) = 2a1+11r⋅ 12 = 6(2a1 + 11r) { 2 100 8 = 2a1 + 3r 672 = 2a1 + 11r.

Odejmujemy od drugiego równania pierwsze i mamy

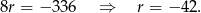
8r = − 33 6 ⇒ r = − 42.

Z drugiego równania

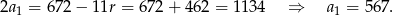
2a = 6 72− 11r = 672 + 46 2 = 1134 ⇒ a = 567. 1 1

Stąd

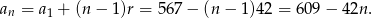
an = a1 + (n− 1)r = 567 − (n − 1 )42 = 609 − 42n .

Sprawdzamy teraz, które wyrazy ciągu 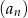(an) są dodatnie.

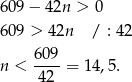
609 − 42n > 0 609 > 42n / : 42 n < 609-= 1 4,5. 42

Najmniejszym dodatnim wyrazem ciągu jest więc

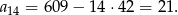
a14 = 609 − 14 ⋅42 = 2 1.

 
Odpowiedź: a1 = 5 67, r = − 42 , a14 = 21

Wersja PDF