/Szkoła średnia/Ciągi

Zadanie nr 8213646

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma nieskończonego zbieżnego ciągu geometrycznego jest równa 56, a suma kwadratów wyrazów tego ciągu jest równa 448. Znajdź pierwszy wyraz tego ciągu i napisz wzór na wyraz ogólny.

Rozwiązanie

Suma wyrazów ciągu geometrycznego 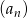(an) daje nam równość

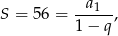
--a1-- S = 5 6 = 1 − q,

gdzie 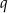q jest ilorazem tego ciągu. Spróbujmy ustalić jak będzie z sumą kwadratów. Ciąg 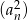2 (an) też jest ciągiem geometrycznym, ale o ilorazie

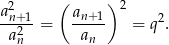
2 ( ) 2 an+1-= an+-1 = q2. a2n an

Mamy więc

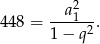
--a21--- 448 = 1 − q2.

Daje to nam układ równań

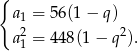
{ a = 5 6(1− q) 1 a21 = 4 48(1− q2).

Podstawiamy z pierwszego równania do drugiego i mamy

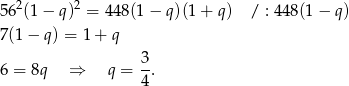
2 2 56 (1 − q) = 4 48(1− q)(1+ q) / : 4 48(1− q) 7(1 − q) = 1 + q 3 6 = 8q ⇒ q = --. 4

Po drodze podzieliliśmy przez 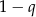1 − q – mogliśmy to zrobić, bo szereg ma być zbieżny, więc 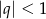|q| < 1 . Mamy ponadto

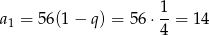
1 a1 = 56(1 − q) = 56 ⋅--= 14 4

oraz

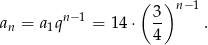
( 3)n −1 an = a1qn− 1 = 14 ⋅ -- . 4

 
Odpowiedź: ( ) a1 = 1 4, an = 14⋅ 3 n−1 4

Wersja PDF