/Szkoła średnia/Ciągi

Zadanie nr 8250015

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wzór na n -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.

Rozwiązanie

Z podanej sumy pierwszych 5 wyrazów mamy równanie

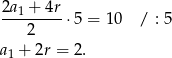
2a + 4r ---1-----⋅5 = 10 / : 5 2 a1 + 2r = 2.

Druga informacja daje nam natomiast

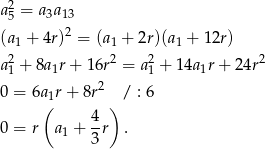
2 a5 = a3a13 2 (a1 + 4r) = (a1 + 2r)(a1 + 12r) a21 + 8a1r+ 16r2 = a21 + 14a1r + 24r2 2 0 = 6a1r + 8r / : 6 ( 4 ) 0 = r a1 + --r . 3

Jeżeli 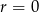r = 0 to dany ciąg jest stały i mamy 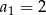a1 = 2 . Zatem an = 2 .

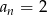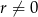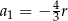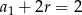Jeżeli natomiast r ⁄= 0 to mamy a1 = − 43r , co podstawiamy do uzyskanej na samym początku równości a1 + 2r = 2 .

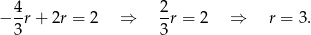
− 4r + 2r = 2 ⇒ 2r = 2 ⇒ r = 3. 3 3

Zatem 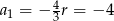a1 = − 43r = −4 i mamy

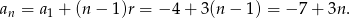
an = a 1 + (n − 1 )r = − 4+ 3 (n− 1) = − 7 + 3n.

 
Odpowiedź: 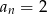an = 2 lub an = 3n − 7

Wersja PDF