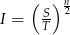Zadanie nr 8287380
Liczby 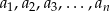 są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a
są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a  jest liczbą parzystą. Znając sumy
jest liczbą parzystą. Znając sumy
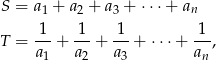
oblicz iloczyn 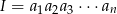 .
.
Rozwiązanie
Jeżeli zapiszemy 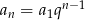 to mamy dane
to mamy dane
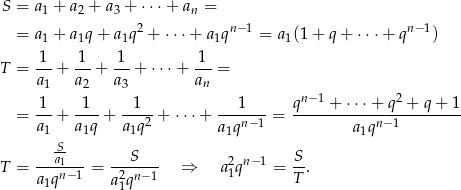
A teraz zobaczmy co mamy obliczyć
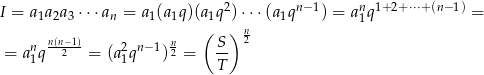
Odpowiedź: 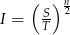
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczby 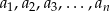 są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a
są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a  jest liczbą parzystą. Znając sumy
jest liczbą parzystą. Znając sumy
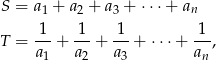
oblicz iloczyn 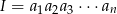 .
.
Jeżeli zapiszemy 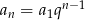 to mamy dane
to mamy dane
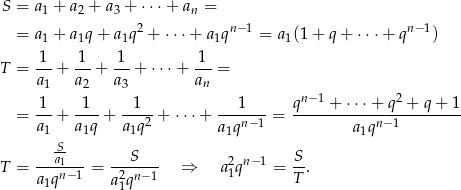
A teraz zobaczmy co mamy obliczyć
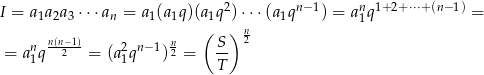
Odpowiedź: