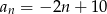/Szkoła średnia/Ciągi

Zadanie nr 8483861

Dodaj do ulubionych
Dodaj do rozwiązanych

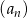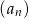Szósty wyraz ciągu arytmetycznego (an) jest o 4 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na n –ty wyraz ciągu (an) , wiedząc, że ciąg 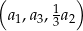( ) a ,a , 1a 1 3 3 2 jest geometryczny.

Rozwiązanie

Korzystając ze wzoru na n –ty wyraz ciągu arytmetycznego mamy

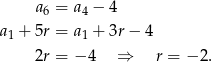
a = a − 4 6 4 a 1 + 5r = a1 + 3r − 4 2r = −4 ⇒ r = − 2.

Mamy stąd

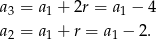
a = a + 2r = a − 4 3 1 1 a2 = a1 + r = a1 − 2 .

Wyraz 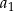a1 obliczymy wykorzystując podaną informację o ciągu geometrycznym.

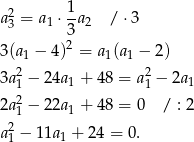
a2= a ⋅ 1a / ⋅ 3 3 1 3 2 3(a − 4)2 = a (a − 2) 1 1 1 3a21 − 24a1 + 48 = a21 − 2a1 2 2a1 − 22a1 + 48 = 0 / : 2 a2− 1 1a + 24 = 0. 1 1

Rozwiązujemy otrzymane równanie kwadratowe.

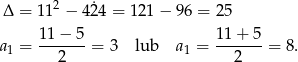
2 ˙ Δ = 11 − 424 = 1 21− 96 = 25 11-−-5- 11-+-5- a 1 = 2 = 3 lub a1 = 2 = 8.

Mamy wtedy odpowiednio

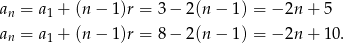
an = a1 + (n− 1)r = 3 − 2(n − 1) = − 2n + 5 an = a + (n− 1)r = 8 − 2(n − 1) = − 2n + 10. 1

 
Odpowiedź: 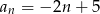an = − 2n + 5 lub an = − 2n + 10

Wersja PDF