Zadanie nr 8635181
Suma trzech liczb tworzących ciąg geometryczny jest równa 63, a ich iloczyn jest równy 5832. Wyznacz ten ciąg.
Rozwiązanie
Sposób I
Jeżeli trzy liczby tworzą ciąg geometryczny, to są one postaci 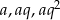 . Mamy zatem układ równań
. Mamy zatem układ równań
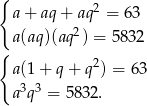
Widać, że musimy wyciągnąć pierwiastek 3 stopnia z liczby 5832. Można łatwo to zrobić dzieląc ją przez sześciany, np. łatwo zauważyć, że dzieli się ona przez 3, więc próbujemy podzielić ją przez 27. Dzieli się też przez 2, więc dzielimy ją przez 8. Otrzymamy w ten sposób 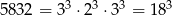 . Mamy zatem
. Mamy zatem
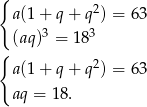
Prowadzi to do równania
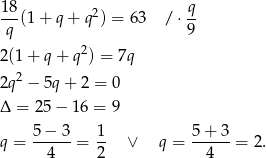
Jeżeli 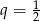 to
to 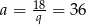 i otrzymujemy ciąg
i otrzymujemy ciąg 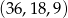 . Jeżeli natomiast
. Jeżeli natomiast 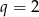 to
to 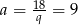 i otrzymujemy ciąg
i otrzymujemy ciąg 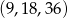 .
.
Sposób II
Szukamy trzech liczb 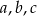 spełniających warunki
spełniających warunki
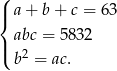
Podstawiamy 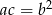 z trzeciego równania do drugiego.
z trzeciego równania do drugiego.
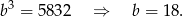
Mamy więc układ równań
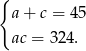
Podstawiamy 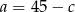 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
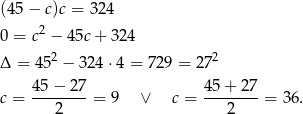
Mamy wtedy 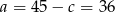 i
i 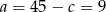 odpowiednio.
odpowiednio.
Odpowiedź: 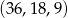 oraz
oraz