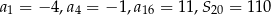/Szkoła średnia/Ciągi

Zadanie nr 8684257

Dodaj do ulubionych
Dodaj do rozwiązanych

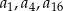Oblicz a1,a4,a 16 oraz sumę 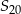S20 dwudziestu pierwszych wyrazów ciągu arytmetycznego 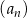(an) jeżeli 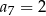a7 = 2 i a9 = 4 .

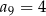Rozwiązanie

Ze wzoru 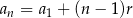an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy układ równań

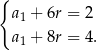
{ a1 + 6r = 2 a + 8r = 4. 1

Odejmując od drugiego równania pierwsze (żeby skrócić 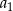a1 ) mamy

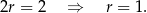
2r = 2 ⇒ r = 1 .

Z pierwszego równania mamy zatem 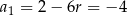a1 = 2 − 6r = −4 . W takim razie

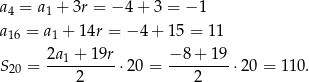
a4 = a1 + 3r = − 4+ 3 = − 1 a16 = a1 + 14r = − 4+ 15 = 11 2a1 + 19r − 8+ 19 S20 = ----------⋅20 = ---------⋅20 = 11 0. 2 2

 
Odpowiedź: a1 = − 4,a4 = −1 ,a16 = 11,S20 = 110

Wersja PDF