/Szkoła średnia/Ciągi

Zadanie nr 8728807

Dodaj do ulubionych
Dodaj do rozwiązanych

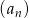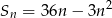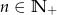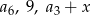Suma n początkowych wyrazów ciągu arytmetycznego (an) wyraża się wzorem Sn = 36n − 3n 2 , gdzie n ∈ N + . Oblicz x wiedząc, że liczby: a6, 9, a 3 + x w podanej kolejności tworzą ciąg geometryczny.

Rozwiązanie

Z podanego wzoru na sumę kolejnych wyrazów ciągu 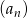(an) obliczamy 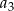a 3 i a6 .

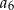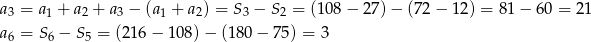
a3 = a1 + a2 + a3 − (a1 + a 2) = S3 − S2 = (108 − 2 7)− (7 2− 12) = 81 − 60 = 2 1 a6 = S6 − S5 = (216− 108) − (180 − 75) = 3

Wykorzystujemy teraz informację o tym, że ciąg 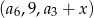(a 6,9 ,a3 + x ) jest geometryczny. W takiej sytuacji kwadrat wyrazu środkowego musi być iloczynem wyrazów sąsiednich.

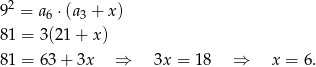
92 = a6 ⋅(a3 + x) 81 = 3(21 + x) 81 = 63 + 3x ⇒ 3x = 18 ⇒ x = 6.

 
Odpowiedź: x = 6

Wersja PDF