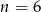Zadanie nr 9134171
Dany jest ciąg arytmetyczny 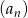 dla
dla 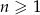 , w którym
, w którym 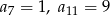 .
.
- Oblicz pierwszy wyraz
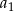 i różnicę
i różnicę  ciągu
ciągu 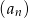 .
. - Sprawdź, czy ciąg
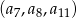 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 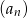 miała wartość najmniejszą.
miała wartość najmniejszą.
Rozwiązanie
- Korzystając ze wzoru na
 -ty wyraz ciągu arytmetycznego mamy układ równań
-ty wyraz ciągu arytmetycznego mamy układ równań 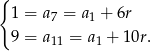
Odejmując od drugiego równania pierwsze (żeby skrócić
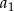 ) mamy
) mamy 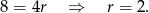
Zatem
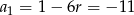 .
.
Odpowiedź: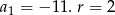
- Wyrazy
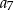 i
i 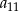 znamy, wyliczmy jeszcze
znamy, wyliczmy jeszcze 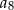
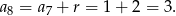
Pytanie zatem brzmi, czy ciąg
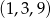 jest geometryczny. Oczywiście jest, z ilorazem
jest geometryczny. Oczywiście jest, z ilorazem 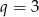 .
.
Odpowiedź: Tak, jest. - Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy
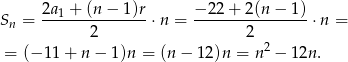
Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, więc wartość najmniejszą przyjmuje dokładnie w środku między pierwiastkami (w wierzchołku), czyli dla
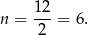
Odpowiedź: