Zadanie nr 9200142
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 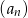 wynosi 6, a suma
wynosi 6, a suma 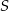 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 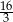 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 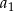 tego ciągu.
tego ciągu.
Rozwiązanie
Z podanych informacji mamy układ równań
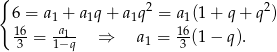
Podstawiamy z pierwszego równania do drugiego i mamy
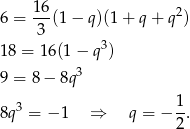
Mamy stąd
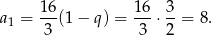
Odpowiedź: