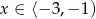Zadanie nr 9400363
Wyznacz wszystkie wartości  , dla których ciąg
, dla których ciąg 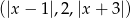 jest malejącym ciągiem arytmetycznym.
jest malejącym ciągiem arytmetycznym.
Rozwiązanie
Trzy liczby 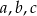 są kolejnymi wyrazami ciągu arytmetycznego wtedy i tylko wtedy, gdy
są kolejnymi wyrazami ciągu arytmetycznego wtedy i tylko wtedy, gdy 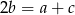 . Musimy rozwiązać więc równanie
. Musimy rozwiązać więc równanie
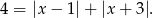
Rozważamy przypadki.
Jeżeli 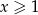 to mamy równanie
to mamy równanie
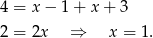
Jeżeli 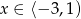 to mamy równanie
to mamy równanie
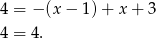
Rozwiązaniem w tym przypadku jest więc cały przedział 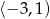 .
.
Jeżeli wreszcie 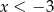 to mamy równanie
to mamy równanie
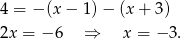
W tym przypadku równanie jest więc sprzeczne.
Ustaliliśmy zatem, że dla dowolnego 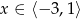 dane trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. To jednak nie koniec, bo ciąg ten ma być malejący. Musi więc być spełniona nierówność.
dane trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. To jednak nie koniec, bo ciąg ten ma być malejący. Musi więc być spełniona nierówność.
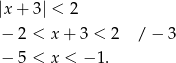
W połączeniu z poprzednim warunkiem otrzymujemy więc 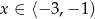 .
.
Drugiej nierówności (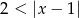 ) nie musimy już sprawdzać, bo jeżeli ciąg jest arytmetyczny to będzie ona spełniona automatycznie.
) nie musimy już sprawdzać, bo jeżeli ciąg jest arytmetyczny to będzie ona spełniona automatycznie.
Odpowiedź: