/Szkoła średnia/Ciągi

Zadanie nr 9440388

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że ciąg liczbowy o wyrazie ogólnym 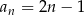an = 2n − 1 , gdzie 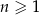n ≥ 1 , jest ciągiem arytmetycznym.

Rozwiązanie

Ciąg 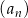(an) jest ciągiem arytmetycznym jeżeli różnica 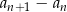an+ 1 − an między dwoma kolejnymi wyrazami jest stała (tzn. nie zależy od n ). Dla danego ciągu mamy

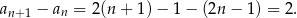
an +1 − an = 2(n + 1) − 1 − (2n − 1 ) = 2.

Jest to zatem ciąg arytmetyczny o różnicy 2.

Wersja PDF