/Szkoła średnia/Ciągi

Zadanie nr 9594409

Dodaj do ulubionych
Dodaj do rozwiązanych

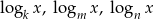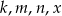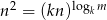Liczby logkx , logm x , logn x są kolejnymi wyrazami ciągu arytmetycznego, gdzie k,m ,n ,x są różnymi od jedności liczbami dodatnimi. Uzasadnij, że n 2 = (kn)logkm .

Rozwiązanie

Sposób I

Zacznijmy od końca, tzn. zlogarytmujmy podaną równość logarytmem przy podstawie 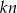kn .

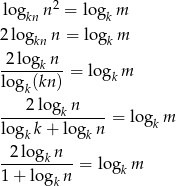
2 logkn n = logk m 2log n = log m kn k -2logk-n-= log m logk(kn ) k 2log n --------k------= lo gkm logk k+ logk n 2 log n ------k--- = logk m 1 + logk n

Mniej więcej widać do czego zmierzamy, więc zacznijmy teraz od początku. Piszemy warunek z ciągiem arytmetycznym (środkowy wyraz jest średnią arytmetyczną sąsiednich).

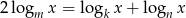
2 lo gm x = logk x+ lo gnx

Aby pozbyć się x musimy zmienić podstawę na wspólną we wszystkich logarytmach. Patrząc na to co ma nam wyjść, zmieniamy podstawę na k .

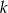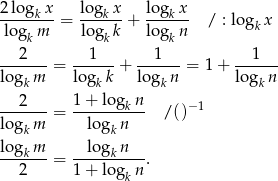
2-logk-x-= logkx-+ logkx- / : log x logk m logkk logkn k 2 1 1 1 -------= ------+ ------= 1 + ------ logkm logkk lo gkn logk n ---2--- 1-+-logkn- −1 log m = log n / () k k logkm-- --logkn--- 2 = 1 + log n . k

No i widać, że jest to dokładnie to, co miało nam wyjść.

Sposób II

Rachunki trochę się upraszczają, jeżeli za wspólną podstawę przyjmiemy 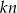kn . Mamy wtedy

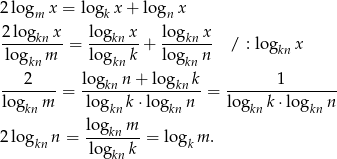
2logm x = logkx + logn x 2 lo g x log x log x -----kn--= ---kn--+ ---kn-- / : lo g x lo gknm logkn k logknn kn 2 log n+ lo g k 1 --------= ---kn--------kn--= --------------- logkn m lo gknk ⋅lo gknn logknk ⋅logknn lo gknm 2logkn n = log--k--= logk m . kn

A to jest dokładnie to, co mieliśmy udowodnić.

Wersja PDF