/Szkoła średnia/Ciągi

Zadanie nr 9621114

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij że w ciągu geometrycznym o parzystej liczbie wyrazów stosunek sumy wyrazów stojących na miejscach parzystych do sumy wyrazów stojących na miejscach nieparzystych jest równy ilorazowi tego ciągu.

Rozwiązanie

Oznaczmy wyrazy danego ciągu przez 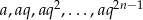2 2n−1 a,aq,aq ,...,aq (wyrazów jest 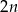2n ). Mamy wtedy

3 2n− 1 2 2n− 2 aq+--aq-+--⋅⋅⋅+-aq------= q(a-+-aq--+-⋅⋅-⋅+-aq-----)= q. a + aq2 + ⋅⋅⋅+ aq2n−2 a+ aq2 + ⋅⋅⋅+ aq 2n−2
Wersja PDF