Zadanie nr 9652526
Ciąg 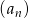 jest określony wzorem
jest określony wzorem
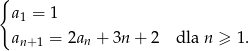
Oblicz średnią arytmetyczną liczb 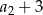 i
i 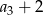 .
.
Rozwiązanie
Obliczamy kolejne wyrazy ciągu.
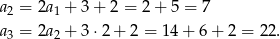
Interesująca nas średnia jest więc równa
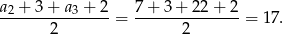
Odpowiedź: 17
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 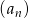 jest określony wzorem
jest określony wzorem
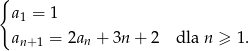
Oblicz średnią arytmetyczną liczb 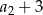 i
i 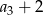 .
.
Obliczamy kolejne wyrazy ciągu.
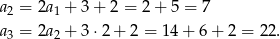
Interesująca nas średnia jest więc równa
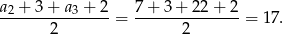
Odpowiedź: 17
