/Szkoła średnia/Ciągi

Zadanie nr 9685571

Dodaj do ulubionych
Dodaj do rozwiązanych

Iloczyn pierwszego i szóstego wyrazu malejącego ciągu arytmetycznego o wyrazach całkowitych jest równy 100. Przy dzieleniu wyrazu drugiego przez wyraz szósty otrzymujemy 3 i resztę 2. Oblicz, o ile jest mniejsza suma dwustu początkowych wyrazów o numerach parzystych od sumy dwustu początkowych wyrazów tego ciągu o numerach nieparzystych.

Rozwiązanie

Zapiszmy najpierw co mamy dane (korzystamy ze wzoru 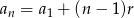an = a1 + (n − 1)r )

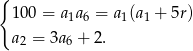
{ 10 0 = a1a6 = a1(a1 + 5r) a2 = 3a 6 + 2 .

Przekształćmy drugie równanie

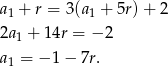
a 1 + r = 3 (a1 + 5r )+ 2 2a 1 + 1 4r = − 2 a 1 = − 1− 7r.

Podstawiamy to do pierwszego równania

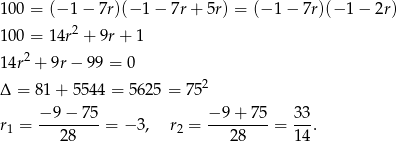
100 = (− 1 − 7r)(− 1 − 7r + 5r) = (− 1 − 7r)(− 1 − 2r) 2 100 = 1 4r + 9r + 1 14r2 + 9r− 99 = 0 Δ = 81+ 5544 = 5 625 = 752 − 9 − 75 − 9 + 75 33 r1 = ---------= − 3, r2 = ---------= ---. 28 28 14

Ponieważ ciąg ma być malejący mamy 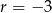r = − 3 i

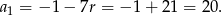
a1 = − 1− 7r = − 1 + 21 = 2 0.

Zastanówmy się co mamy policzyć:

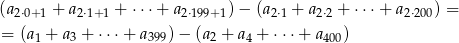
(a2⋅0+1 + a2⋅1+1 + ⋅⋅⋅+ a 2⋅199+1)− (a2⋅1 + a2⋅2 + ⋅⋅⋅ + a2⋅200) = = (a 1 + a3 + ⋅⋅⋅ + a399)− (a 2 + a4 + ⋅⋅⋅ + a400)

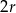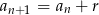Możemy to wyrażenie obliczyć na różne sposoby, np. zauważając, że oba ciągi w nawiasach są arytmetyczne z różnicą 2r . Najprościej jest jednak skorzystać z tego, że an+1 = an + r .

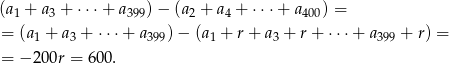
(a1 + a3 + ⋅⋅⋅+ a399) − (a2 + a4 + ⋅⋅⋅+ a400) = = (a1 + a3 + ⋅⋅⋅+ a399) − (a1 + r+ a3 + r+ ⋅⋅⋅ + a399 + r) = = − 200r = 600.

 
Odpowiedź: Jest mniejsza o 600

Wersja PDF