/Szkoła średnia/Ciągi

Zadanie nr 9709692

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym trójkątnym wysokość podstawy, krawędź podstawy i wysokość graniastosłupa tworzą ciąg geometryczny. Oblicz długość krawędzi podstawy graniastosłupa wiedząc, że jego objętość jest równa 108.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy krawędź podstawy przez a .

PIC

Sposób I

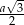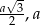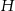Ponieważ wysokość trójkąta równobocznego o boku a ma długość √ - a-3- 2 , z podanej informacji, że liczby a√3- 2 ,a i H są kolejnymi wyrazami ciągu geometrycznego mamy

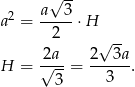
√ -- a2 = a--3-⋅H 2 2a 2√ 3a H = √---= ------. 3 3

Pora wykorzystać informację o tym, że objętość graniastosłupa wynosi 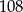10 8

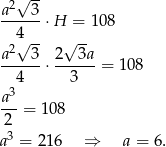
√ -- a2--3- 4 ⋅H = 108 2√ -- √ -- a---3-⋅ 2-3a-= 108 4 3 a3 ---= 10 8 23 a = 216 ⇒ a = 6.

Sposób II

Jeżeli przez 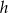h oznaczymy wysokość podstawy, to objętość graniastosłupa jest równa

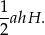
1ahH . 2

Z podanej informacji o ciągu geometrycznym wiemy, że 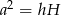a2 = hH , zatem

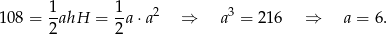
1 08 = 1-ahH = 1-a⋅a 2 ⇒ a3 = 216 ⇒ a = 6. 2 2

 
Odpowiedź: a = 6

Wersja PDF