/Szkoła średnia/Ciągi

Zadanie nr 9786143

Dodaj do ulubionych
Dodaj do rozwiązanych

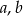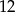O liczbach a ,b i c wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi 12 . Wyznacz największą możliwą wartość wyrażenia 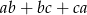ab+ bc+ ca . Dla jakich liczb 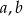a,b i c wartość ta jest osiągana.

Rozwiązanie

Możemy założyć, że 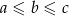a ≤ b ≤ c . Zatem 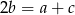2b = a+ c oraz

12 = a + b + c = 3b ⇒ b = 4, a + c = 8 .

Szukamy największej możliwej wartości funkcji

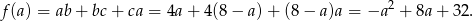
2 f(a) = ab + bc + ca = 4a + 4 (8− a )+ (8 − a)a = −a + 8a + 3 2.

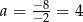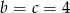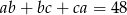Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w dół, największa wartość jest osiągana w wierzchołku paraboli, czyli w punkcie −8- a = −2 = 4 . Wtedy b = c = 4 i ab+ bc+ ca = 48 .  
Odpowiedź: Największa wartość 48 dla liczb (a,b,c) = (4 ,4,4)

Wersja PDF