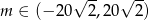/Szkoła średnia/Ciągi

Zadanie nr 9977327

Dodaj do ulubionych
Dodaj do rozwiązanych

Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 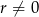r ⁄= 0 są kolejnymi wyrazami ciągu geometrycznego o ilorazie 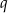q . Dla jakich wartości parametru 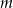m funkcja 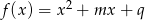f(x ) = x2 + mx + q osiąga minimum większe od − 196 ?

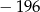Rozwiązanie

Oznaczmy trzy wyrazy ciągu arytmetycznego, o których mowa w zadaniu, przez 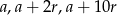a ,a+ 2r ,a + 1 0r . Mamy wtedy

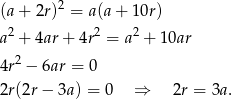
2 (a + 2r) = a(a + 10r) a2 + 4ar + 4r2 = a2 + 10ar 4r2 − 6ar = 0 2r(2r − 3a) = 0 ⇒ 2r = 3a.

Zatem

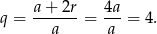
a+ 2r 4a q = ------ = ---= 4. a a

Minimum funkcji 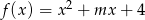f(x ) = x2 + mx + 4 to dokładnie druga współrzędna wierzchołka paraboli będącej wykresem 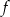f . Mamy więc nierówność

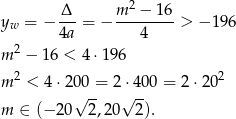
Δ m 2 − 16 yw = − ---= − -------- > − 196 4a 4 m 2 − 1 6 < 4⋅ 196 2 2 m < 4⋅ 200-= 2 ⋅400 = 2 ⋅20 m ∈ (−2 0√ 2,20√ 2).

 
Odpowiedź: √ -- √ -- m ∈ (− 20 2,20 2)

Wersja PDF