/Szkoła średnia/Statystyka/Dane z tabeli

Zadanie nr 4187738

Tabela zawiera niektóre wyniki pisemnego sprawdzianu z matematyki w pewnej klasie maturalnej (ocenionego w sześciostopniowej skali ocen).

  Dziewczęta Chłopcy
liczba osób 11 14
średnia ocen 4,0 3,8
odchylenie standardowe 1,1 1,8

Oblicz średnią ocen z tego sprawdzianu oraz odchylenie standardowe dla całej klasy. Wyniki podaj z zaokrągleniem do jednego miejsca po przecinku.

Wersja PDF

Rozwiązanie

Sposób I

Z podanych średnich wynika, że suma ocen dziewcząt jest równa

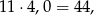
1 1⋅4,0 = 44,

a suma ocen chłopców jest równa

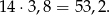
14 ⋅3,8 = 53,2.

Tu powinno nas coś zastanowić, jak to możliwe, że suma ocen jest równa 53,2, skoro sprawdzian był oceniany w sześciostopniowej skali? Oczywiście nie może, a 53,2 powstało w wyniku zaookrąglenia średniej. Policzmy średnią przy "sąsiednich" sumach

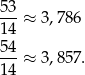
53- 14 ≈ 3,786 54 ---≈ 3,857. 14

Widać zatem, że suma ocen chłopców musiała być równa 53.

W takim razie średnia ocen całej klasy jest równa

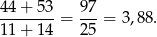
44 + 53 97 --------= ---= 3,88. 11 + 14 25

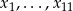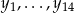Spróbujmy teraz policzyć sumę kwadratów odchyleń ocen dziewcząt i chłopców. Jeżeli przez x1,...,x 11 i y1,...,y 14 oznaczymy oceny uzyskane przez dziewczynki i chłopców to wiemy, że

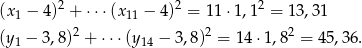
(x1 − 4)2 + ⋅⋅⋅(x11 − 4)2 = 11 ⋅1,12 = 13,31 2 2 2 (y1 − 3,8) + ⋅⋅⋅(y14 − 3,8) = 1 4⋅1,8 = 45,36.

Liczymy teraz sumy kwadratów odchyleń, ale od średniej całej klasy. Najpierw dla dziewczynek

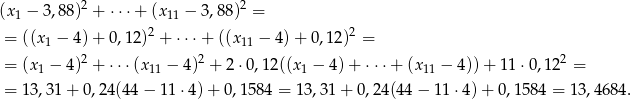
2 2 (x1 − 3,88) + ⋅⋅⋅+ (x11 − 3 ,88) = 2 2 = ((x1 − 4) + 0,12) + ⋅⋅⋅+ ((x11 − 4)+ 0 ,12) = = (x1 − 4)2 + ⋅⋅⋅(x11 − 4)2 + 2⋅ 0,12((x1 − 4)+ ⋅⋅⋅+ (x11 − 4 ))+ 11 ⋅0,12 2 = 13,31 + 0,2 4(44− 11⋅ 4)+ 0,1584 = 1 3,31+ 0,24(44 − 11 ⋅4) + 0,158 &

Podobnie liczymy sumę kwadratów odchyleń ocen chłopców od średniej

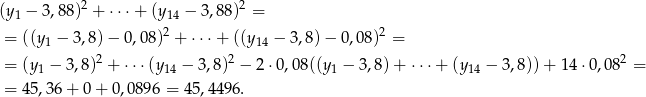
2 2 (y1 − 3,88) + ⋅⋅⋅+ (y14 − 3 ,8 8) = = ((y1 − 3,8) − 0,08)2 + ⋅⋅⋅+ ((y14 − 3,8)− 0,08)2 = 2 2 2 = (y1 − 3,8) + ⋅⋅⋅(y14 − 3,8) − 2 ⋅0,08((y1 − 3,8) + ⋅⋅⋅+ (y14 − 3,8))+ 14 = 45,36 + 0 + 0,08 96 = 45,44 96.

Zatem wariancja ocen całej klasy jest równa

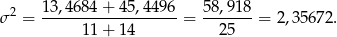
13,4684 + 45,4 496 58,918 σ2 = -------------------= -------= 2,35672 . 11 + 14 25

Pozostało policzyć odchylenie standardowe

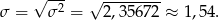
√ --- √ -------- σ = σ2 = 2,356 72 ≈ 1,54.

Sposób II

Tym razem nie przejmujmy się poprawnością podanych danych i postarajmy się jak najszybciej wyliczyć żądane wartości.

Oznaczmy przez 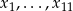x1,...,x 11 oceny dziewcząt, a przez 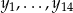y1,...,y14 oceny chłopców. Z podanych średnich mamy

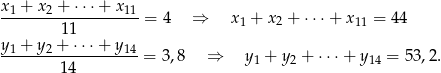
x1 + x2 + ⋅⋅⋅+ x11 ------------------- = 4 ⇒ x 1 + x 2 + ⋅ ⋅⋅+ x11 = 44 y + y 1+1⋅⋅⋅+ y -1----2----------14= 3,8 ⇒ y 1 + y 2 + ⋅⋅ ⋅+ y14 = 53,2 . 14

Stąd wyliczamy średnią s wszystkich ocen

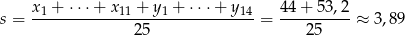
s = x1 +-⋅⋅⋅+-x-11-+-y1-+-⋅⋅⋅+--y14-= 4-4+--53,2 ≈ 3,8 9 25 25

Różnica w stosunku do poprzedniego sposobu wynika oczywiście z błędu przybliżenia.

Wariancję wyliczymy korzystając ze wzoru

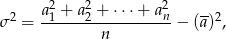
a2 + a2 + ⋅⋅⋅+ a2n -- σ 2 = -1----2-----------− (a)2, n

gdzie 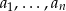a ,...,a 1 n są danymi, a 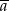a- ich średnią.

Na mocy powyższego wzoru i podanych danych mamy

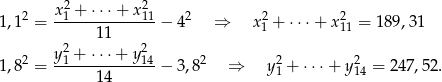
x2 + ⋅⋅⋅ + x2 1,12 = -1----------11 − 42 ⇒ x12+ ⋅⋅⋅ + x211 = 189 ,31 11 2 y21 + ⋅⋅⋅ + y214 2 2 2 1,8 = ------14------ − 3,8 ⇒ y1 + ⋅⋅⋅ + y14 = 247 ,5 2.

Liczymy teraz wariancję wszystkich danych.

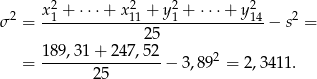
2 2 2 2 σ 2 = x1-+-⋅⋅⋅+--x11 +-y1 +-⋅-⋅⋅+-y14-− s2 = 25 189,31 + 2 47,52 2 = -------25--------− 3,89 = 2,3411.

Stąd odchylenie standardowe jest równe

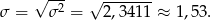
√ --- ------- σ = σ2 = √ 2,3411 ≈ 1 ,53.

 
Odpowiedź: Średnia: 3,9, odchylenie: 1,5

Wersja PDF