/Szkoła średnia/Statystyka/Dane z tabeli

Zadanie nr 5215671

Tabela przedstawia dane dotyczące wieku kobiet i mężczyzn pracujących w małej firmie zatrudniającej 7 osób:

  Kobiety Mężczyźni
Liczba osób 3 4
Średni wiek 26 33
Odchylenie standardowe 1,4 4,6

Wyznacz średnie odchylenie standardowe liczone dla wszystkich osób pracujących w tej firmie.

Wersja PDF

Rozwiązanie

Będziemy korzystać z następującego wzoru na wariancję:

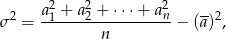
2 2 2 σ 2 = a1-+-a2-+-⋅⋅⋅+--an− (a)2, n

gdzie 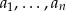a1,...,an są danymi, a 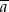-- a ich średnią.

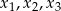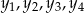Oznaczmy przez x1,x 2,x3 i y1,y2,y3,y4 liczby lat odpowiednio kobiet i mężczyzn pracujących w firmie. Wtedy na mocy powyższego wzoru i podanych danych mamy

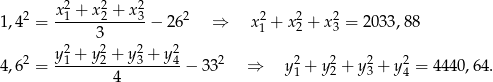
2 x21 + x22 + x23 2 2 2 2 1,4 = -------------− 26 ⇒ x 1 + x 2 + x 3 = 2033,8 8 2 32 2 2 2 y1 +-y2 +-y3 +-y4- 2 2 2 2 2 4,6 = 4 − 33 ⇒ y1 + y2 + y3 + y4 = 4 440,64.

Mając obliczone sumy kwadratów danych, jesteśmy bliscy obliczenia wariancji wszystkich danych (ze wzoru na początku rozwiązania), ale wciąż brakuje nam średniej s wszystkich danych. Z podanych średnich mamy

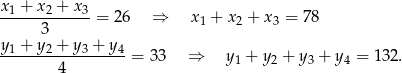
x1 +-x2 +-x3-= 26 ⇒ x + x2 + x3 = 78 3 1 y1 +-y2 +-y-3 +-y-4 4 = 33 ⇒ y 1 + y 2 + y 3 + y4 = 132.

Zatem średnia jest równa

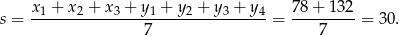
x + x + x + y + y + y + y 78+ 132 s = -1----2----3----1----2----3----4 = ---------= 3 0. 7 7

Liczymy wariancję

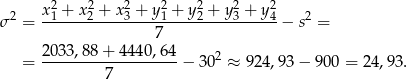
x2+ x2+ x2+ y2+ y2+ y2+ y2 σ2 = -1----2----3----1----2----3----4-− s2 = 7 2033,88-+-4-440,64- 2 = 7 − 30 ≈ 924,93 − 900 = 24,93.

Stąd odchylenie standardowe jest równe

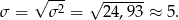
√ --- √ ------ σ = σ 2 = 24,93 ≈ 5.

 
Odpowiedź: 5

Wersja PDF