/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I 9 marca 2016 Czas pracy: 170 minut
Zadania zamknięte
Odwrotnością liczby 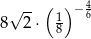 jest liczba
jest liczba
A) 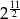 B)
B) 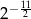 C)
C) 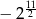 D)
D) 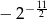
Różnica liczby  i jej kwadratu jest największa dla liczby
i jej kwadratu jest największa dla liczby  równej
równej
A) 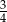 B)
B) 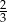 C)
C) 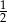 D)
D) 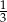
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 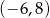 .
.
A) 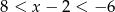 B)
B) 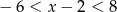 C)
C) 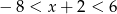 D)
D) 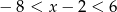
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Liczba o 3 większa od 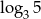 jest równa
jest równa
A) 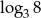 B)
B) 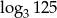 C)
C) 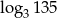 D)
D) 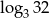
Na wykresie funkcji liniowej określonej wzorem 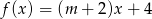 leży punkt
leży punkt 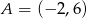 . Zatem
. Zatem
A) 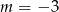 B)
B) 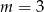 C)
C) 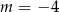 D)
D) 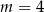
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
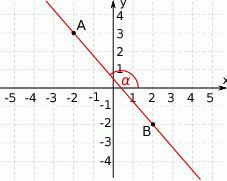
A)  B)
B) 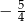 C)
C)  D)
D) 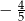
Prosta o równaniu 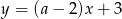 jest prostopadła do prostej
jest prostopadła do prostej 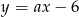 . Zatem
. Zatem
A) 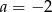 B)
B) 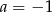 C)
C) 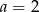 D)
D) 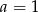
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest
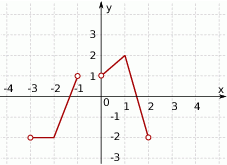
A) 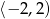 B)
B) 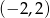 C)
C) 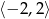 D)
D) 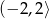
Dziedziną funkcji 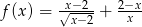 jest
jest
A) 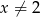 B)
B) 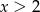 C)
C) 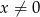 D)
D) 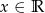
Jeżeli długość przekątnej sześcianu wynosi 3, to pole powierzchni całkowitej tego sześcianu jest równe
A) 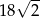 B) 24 C)
B) 24 C) 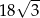 D) 18
D) 18
Funkcja kwadratowa określona jest wzorem 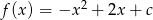 . Jeżeli
. Jeżeli 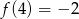 , to
, to
A) 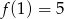 B)
B) 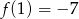 C)
C) 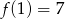 D)
D) 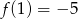
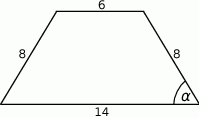
Dany jest trapez równoramienny (patrz rysunek). Wtedy 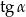 jest równy
jest równy
A) 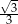 B)
B) 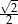 C)
C) 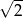 D)
D) 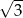
Punkty 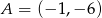 i
i 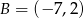 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 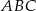 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 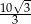 B)
B) 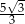 C)
C) 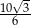 D)
D) 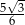
Dana jest funkcja 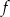 określona wzorem
określona wzorem 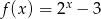 . Wartość funkcji
. Wartość funkcji  dla argumentu
dla argumentu 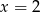 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Dla jakiej całkowitej wartości liczby  spełniona jest nierówność
spełniona jest nierówność 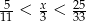 ?
?
A) 4 B) 3 C) 2 D) 1
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 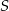 wynosi
wynosi
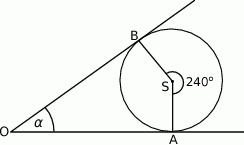
A) 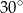 B)
B) 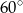 C)
C) 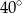 D)
D) 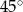
Miary kątów czworokąta tworzą ciąg arytmetyczny o pierwszym wyrazie 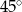 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 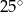 B)
B) 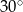 C)
C) 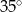 D)
D) 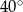
Doświadczenie losowe polega na trzykrotnym rzucie monetą. Prawdopodobieństwo, że dokładnie dwa razy wylosujemy orła wynosi
A)  B)
B) 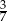 C)
C)  D)
D) 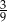
Dany jest ciąg liczbowy 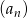 , w którym
, w którym 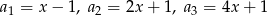 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem arytmetycznym?
dany ciąg jest ciągiem arytmetycznym?
A) 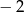 B) 2 C) 3 D) 4
B) 2 C) 3 D) 4
Ze zbioru liczb naturalnych dwucyfrowych nie większych niż 35 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 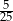 B)
B) 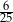 C)
C) 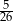 D)
D) 
Dla jakich argumentów funkcja 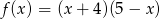 przyjmuje wartości nieujemne?
przyjmuje wartości nieujemne?
A) 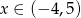 B)
B) 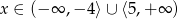 C)
C) 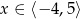 D)
D) 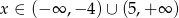
Kąty 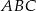 i
i 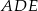 są równe oraz
są równe oraz 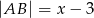 ,
, 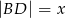 ,
, 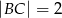 ,
, 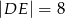 . Wobec tego
. Wobec tego  jest równe
jest równe
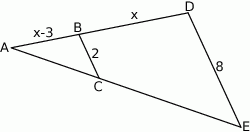
A) 3 B) 3,5 C) 4 D) 4,5
Przekątne trapezu 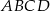 o podstawach
o podstawach 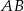 i
i 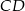 przecinają się w punkcie
przecinają się w punkcie 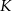 w ten sposób, że
w ten sposób, że 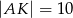 ,
, 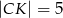 ,
, 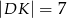 . Długość odcinka
. Długość odcinka 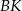 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
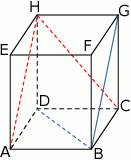
Podstawą graniastosłupa prostego czworokątnego 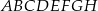 jest kwadrat
jest kwadrat 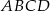 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 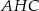 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 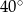 . Kąt
. Kąt 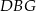 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
A) 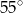 B)
B) 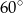 C)
C) 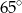 D)
D) 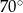
Zadania otwarte
Funkcja kwadratowa 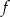 , której miejscami zerowymi są liczby
, której miejscami zerowymi są liczby 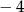 i 6, dla argumentu 1 przyjmuje wartość
i 6, dla argumentu 1 przyjmuje wartość 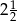 . Uzasadnij, że wykres funkcji
. Uzasadnij, że wykres funkcji 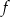 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą 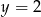 .
.
Rozwiąż nierówność kwadratową 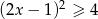 .
.
W trójkącie prostokątnym przyprostokątne mają długości 2 i 4, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 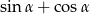 .
.
Wykres funkcji kwadratowej 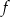 danej wzorem
danej wzorem 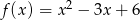 przecięto prostymi o równaniach
przecięto prostymi o równaniach 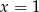 oraz
oraz 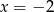 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji
. Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji 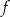 .
.
Różnica współczynników kierunkowych dwóch prostych jest równa różnicy odwrotności tych współczynników. Uzasadnij, że te proste są prostopadłe albo równoległe.
Oblicz pole trójkąta 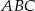 , którego boki zawierają się w prostych o równaniach:
, którego boki zawierają się w prostych o równaniach: 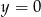 ,
, 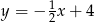 oraz
oraz 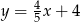 .
.
Tworząca stożka o kącie rozwarcia  ma długość 8. Pole powierzchni całkowitej tego stożka jest równe
ma długość 8. Pole powierzchni całkowitej tego stożka jest równe 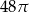 . Oblicz objętość stożka oraz miarę kąta
. Oblicz objętość stożka oraz miarę kąta  .
.
Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę białą. Wynik przedstaw w postaci ułamka nieskracalnego.
W roku 2016 na uroczystości urodzinowej ktoś zapytał jubilata, które urodziny obchodzi. Jubilat odpowiedział: jeżeli mój wiek sprzed 36 lat pomnożysz przez mój wiek za 55 lat, to otrzymasz rok mojego urodzenia. Oblicz, ile lat ma ten jubilat.

