Zadanie nr 7373983
Proste 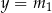 i
i 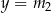 , gdzie
, gdzie 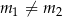 są styczne do wykresu funkcji
są styczne do wykresu funkcji 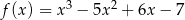 w punktach
w punktach 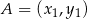 i
i 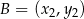 . Zatem
. Zatem
A) 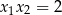 B)
B) 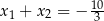 C)
C) 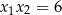 D)
D) 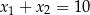
Rozwiązanie
Jeżeli styczna do wykresu danej funkcji jest pozioma w pewnym punkcie, to pochodna w tym punkcie jest równa 0.
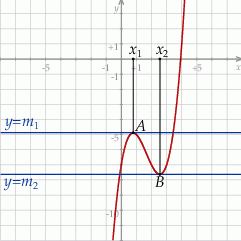
W takim razie liczby 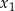 i
i 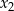 są miejscami zerowymi pochodnej:
są miejscami zerowymi pochodnej:
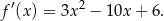
Na mocy wzorów Viète’a mamy
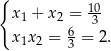
Odpowiedź: A

